
The principle of induction is one of Peano's axioms.
The principle of induction states any set $S$ of natural numbers that includes $0$ as an element, and has the property that for every natural number $n$ in $S$, $n+1$ is also in $S$, then $S$ is isomorphic with $\naturals$, the set of natural numbers.
The above can be expressed as an axiom in one of two ways. The direct axiomatic statment simply states the above:
For any set $S$ of natural numbers ($S \subset \naturals$), if $0$ is an element of the set and, if for every natural number $n$ in $S$, $n+1$ is also in the set, then $S = \naturals$.
A variant of the axiom of induction is the axiom of strong induction.
Let $S \subset \naturals$ be any subset of $\naturals$ with the following properties:
then, $S = \naturals$.
Note that this differs from the simpler axiom of induction in that it requires all numbers less than or equal to $n$ (and not just $n$ itself) to be in $S$ for $n+1$ to also be in $S$. The difference between the two is explained in the figure below.

The axiom of strong induction is actually strictly equivalent to the weaker axiom that only requires $n \in S$, and the two can be derived from one another. However, sometimes the axiom of strong induction provides an easier mechanism for some proofs. We will see an example below.
An alternate, but equivalent axiom is the axiom of well ordering.
$\naturals$ is well ordered.
Recall that a well-ordered set is one in which every subset has a smallest element. The axiom of well ordering states that every subset of $\naturals$ has a smallest element. This is not an obvious statement, and cannot be derived from any of the other axioms.We only need one of the two above axioms. If we assume induction to be an axiomatic property, then the well ordering of $\naturals$ can be derived from the axiom of induction. On the other hand, if we assume the axiom of well ordering, then the principle of induction can be derived from it. Lets consider the two below.

Let $S$ be a subset of $\naturals$ such that $0 \in S$ and $\forall n\in \naturals~ (n \in S \Rightarrow n+1\in S)$. We must prove that $S = \naturals$.
Proof:
We will employ proof by contradiction. Assume $S \neq \naturals$. This implies that there are elements of $\naturals$ that are not in $S$. For instance, the Figure above shows a possible set of natural numbers (in red) which may belong to $S$. The rest are not in $S$.
Let $Y = \naturals\setminus S$ be the set of natural numbers that are not in $S$.
Since, by axiom, $\naturals$ is well ordered, every subset of $\naturals$ must have a least element. Let $x \in Y$ be the least element of $Y$. Since $0 \in S$, $x > 0$.
From the remaining axioms, we know that $x$ has a predecessor $y$, such that $x = y+1$. Also, since $x$ is the least element of $Y$, $y \notin Y$. Therefore $y \in S$.
However, from the successor property of $S$, $y \in S \Rightarrow y+1 \in S \Rightarrow x \in S$. Therefore $x \notin Y$, which is a contradiction of our definition of $Y$.
Alternately stated, $Y$ cannot have a least element, and therefore $Y$ is empty, implying that $\naturals \setminus S = \emptyset$, i.e. $S = \naturals$.
Proof:
Here we will assume induction to be true, and prove that $\naturals$ must be well ordered. Once again we use proof by contradiction.
Let $S \subset \naturals$ be any subset of $\naturals$ without a least element. We will show that $S$ cannot exist, or if it does, it is empty.
Let $Y = \naturals \setminus S$ be the set of all natural numbers not in $S$. To show that $S$ must be empty, it is enough to show that $Y = \naturals$. Note that $S = \naturals \setminus Y$.
We note that $n=0$ is an element of $\naturals$, and $0$ is the least element of $\naturals$. So, clearly $0\notin S$, because if $0 \in S$, $0$ would be the least element of $S$ and $S$ has no least element. As a consequence $0 \in $Y$.
For any $n$ assume that all $m \leq n \in Y$, i.e. all natural numbers from $0$ until $n$ are in $Y$. Then, $n+1$ cannot be in $S$, because if $n+1$ were in $S$, it would be the least element of $S$, but $S$ has no least element. This implies that $n+1 \in Y$.
Using the axiom of strong induction this implies that $Y = \naturals$, implying that $S = \naturals \setminus Y = \emptyset$.
Although we have sloppily stated that $S = \naturals$ above, to be more precise, the true claim is that $S$ is isomorphic with $\naturals$, i.e. it has a one-to-one correspondence with $\naturals$. So, for instance, if $S$ is a set where we only have the base case that $7 \in S$, and for all $n$, $n\in S \Rightarrow n+1 \in S$, then $S = \{7, 8, 9, \cdots\}$. This is not $\naturals$, but has an exact one-to-one correspondence with $\naturals$.
In the proof technique of mathematical induction that we describe below, we will often use base cases of $1 \in S$, rather than $0 \in S$, and sometimes, depending on the problem, other numbers may be used as well.
As a consequence of the axiom of induction, this implies that the set of natural for which $\mathcal{H}$ holds true is all of $\naturals$.
The principle of induction, although not stated explicitly as such, has been used to prove hypotheses for well over 2000 years!
From Wikipedia: In 370 BC, Plato's Parmenides may have contained an early example of an implicit inductive proof. The earliest implicit traces of mathematical induction can be found in Euclid's proof that the number of primes is infinite.
Lets consider a couple of examples below.
Proof:
We are required to prove that $H(n) = 1 + 3 + 5 + 7 + .. + (2n-1) = n^2$.
Base case:
Consider $n = 1$. $2n-1 = 1$. $1 = 1^2$. The proposition holds true for $n = 1$.
Induction Step:
Let the proposition be true for any $n$. Consider the $n+1$ case. \[ H(n+1) = 1 + 3 + 5 + 7 + \cdots + (2(n+1)-1) = 1 + 3 + 5 + 7 + \cdots + (2n-1) + (2(n+1)-1) = H(n) + (2n+1) \]
By our assumption, $H(n) = n^2$. Therefore \[ H(n+1) = n^2 + 2n + 1 = (n+1)^2 \]
which shows that the proposition holds true for $n+1$ as well.
Thus, from the principle of induction, the proposition holds true for all $n \geq 1$.
The manner in which the induction step is set up is important. We must set up the $n+1$ case and identify the $n$ cases in it to prove the statement. The opposite approach, of setting up the $n$ case and extending it to $n+1$ by construction will often be wrong, because we would only have proved our statement for the specific $n+1$ case that we constructed from the $n$ case.
In the above proof, note that we followed this principle and set up $H(n+1)$, which we then decomposed into $H(n)$ and some additional terms.
The importance of this mechanism is more clear in the following problem.
The proposition states that we can fill in any chess board of size $2^n \times 2^n$ almost entirely, leaving only one square unoccupied, using pieces of the following shape:

The figure below illustrates this for a simple case of $n=1$.
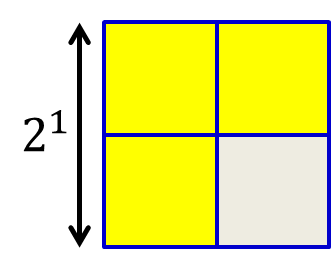
Proof:
Base Case:
The base case for $n=1$ has already been shown in the above figure. The proposition holds true for $n=1$.
Inductive Step:
Assume that for any board of size $2^n$ the proposition holds. Furthermore, assume that the board can be composed of L-shapes such that the single empty square is at a corner. (We will leave the proof that if any board of size $2^n$ can be filled by L-shapes leaving out only one square, then it can be done so that the blank square is at a corner, for the reader to prove. This too needs induction).
Consider now a square of size $2^{n+1}$. This can be decomposed into four squares of size $2^n$ as shown below. Each of the four can be filled using L-shape blocks, leaving one square free in each. The four $2^n$-sized squares can then be arranged with their empty blocks aligned as shown in the figure.
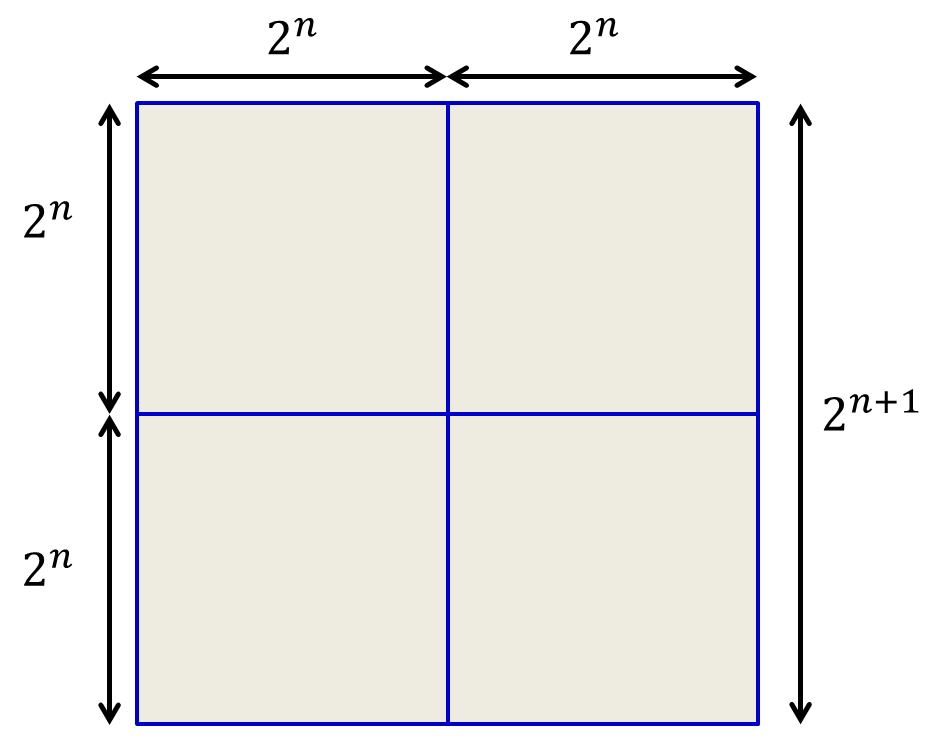
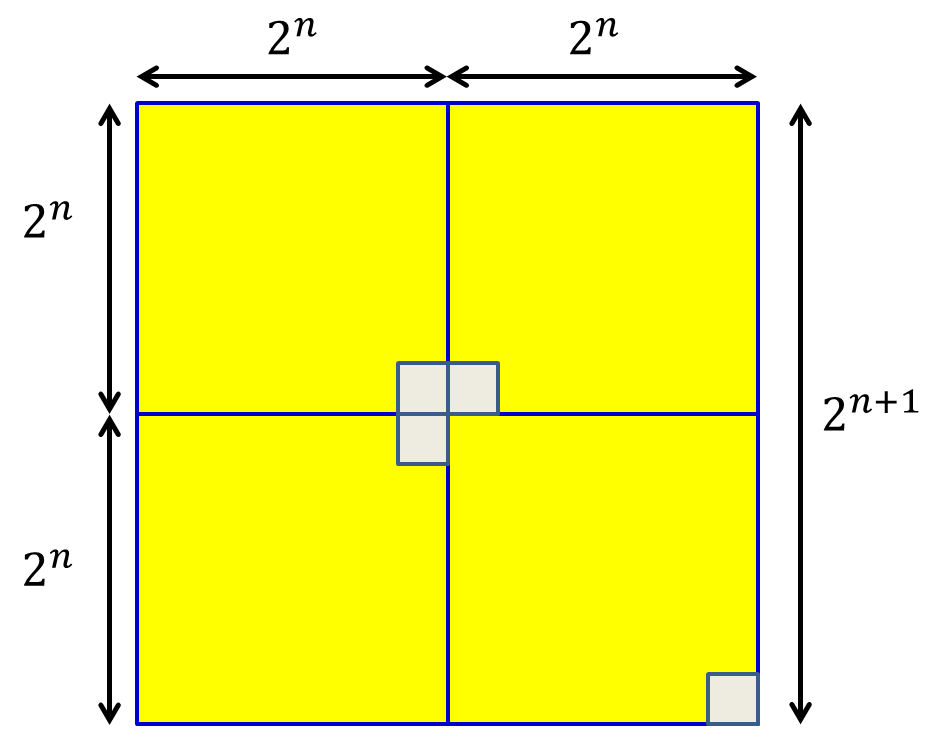
The three blanks from the original $2^n$-sized blocks align up in an L, and can be filled by an L-shape, leaving being a $2^{n+1}$ square that is entirely filled with L-shaped blocks, leaving only one square free in the corner.
Thus, if any $2^n$-square board can be filled using L-shapes leaving only a corner square empty, a $2^{n+1}$-square board can also be similarly filled as proposed. We have already shown the base case that the proposition holds for $n=1$. Thus, from the principle of induction, the proposition holds for all $n$.