How to measure the distance? Here we introduce a common method: Metric Spaces.
A set $\mathbb{X}$ is a metric space, if any two point p and q of $\mathbb{X}$ can be assigned to a function $d(p, q): \mathbb{X} \times \mathbb{X} \rightarrow \mathbb{R}$ (called a "metric" or, a "distance function"), satisfying the properties:
1. Non-negative: $d(p, q) \ge 0$ if $p \not= q$, and $d(p, q) = 0$ iff $p = q$,
2. Symmetric: $d(p, q) = d(q, p)$,
3. Triangle Inequality: $d(p, r) + d(r, q) \ge d(p, q)$, for any $r \in \mathbb{X}$.
Metric space is fully represented by as $(\mathbb{X}, d)$, in which $\mathbb{X}$ is a set and d is a metric.
For example: $(\reals ^ n, Edclidean)$ is very usual. How about $(\mathbb{X}, Discrete)$, Discrete like \begin{equation} d(p,q)= \begin{cases} 0 &\mbox{$p = q$}\\ 1 &\mbox{$p \not= q$} \end{cases} \end{equation}
The third property "$d(p, r) + d(r, q) \ge d(p, q)$" is called Triangle Inequality in $R^2$ metric, it is, the sum of any two sides of a triangle is not less than the third side.
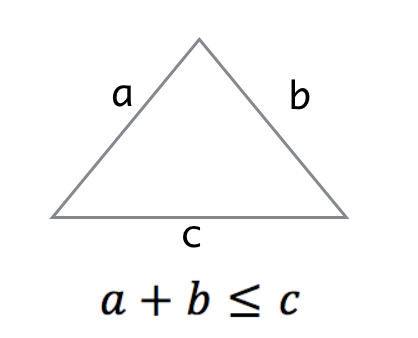
One of the most important examples of metric spaces is Edclidean Spaces $R^k$.
$R^1$ (the real line): $d(x, y) = |x - y|$,
$R^2$ (the complex plane): $d(x, y) = \sqrt{|x_1 - y_1|^2 + |x_2 - y_2|^2}$,
$R^k$ : $d(x, y) = \sqrt{|x_1 - y_1|^2 + \dots + |x_k - y_k|^2}$.
$d(x, y)$ is called edclidean metric, and $(R^n, d)$ is called edclidean space.
Function defined on [a,b]:
$d(f,g) = \int_a^b |f(x) - g(x)| {\rm d}x$,
$d(f,g) = SUP_{x \in [a,b]} |(f(x) - g(x)|$.