\( \def\naturals{\mathbb{N}} \def\integers{\mathbb{Z}} \def\rationals{\mathbb{Q}} \def\reals{\mathbb{R}} \)

Cantor Set

Definition

Given the interval $[0,1]$, removing the open middle third $(\frac{1}{3}, \frac{2}{3})$, removing the middle third of each of $[0, \frac{1}{3}]$ and $[\frac{2}{3}, 1]$, and continuing to infinitum.

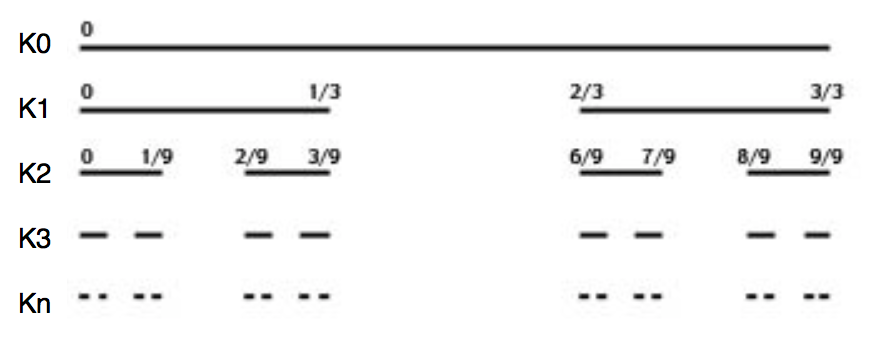
triangle_inequality

Cantor Set: $\mathbb{C} = \cap^\infty_{n=0} K_n$

Properities

Cantor set is a perfect set (closed and every point of $\mathbb{C}$ is a limit point of $\mathbb{C}$).

Cantor set is uncountable.

Cantor set is totally disconnected.

Cantor set consistes of real numbers, whose terrany expansion contains only 0 or 2.